

Now, it is used routinely to model the behaviour of electrons, atoms and molecules. This is a complicated theory which developed over time following a great deal of experimental input. Hence, conservation of energy is the correct answer.The structures of atoms are described by quantum mechanics. This operator is equated to the sum of kinetic energy and potential energy of the quantum system. Question 5: Schrodinger equation is based on _.Įxplanation: In the Schrödinger equation, the Hamilton operator gives the total energy of the system.
SCHRODINGER EQUATION FOR HYDROGEN FREE
The free particle has maximum kinetic energy. Question 4: For a free particle, _ is zero.Įxplanation: A particle is said to be a free particle when the net potential energy is zero. It indicates the region of space in which the particle is more likely to be found. The Schrodinger equation is linear partial differential equation that describes the evolution of a quantum state in a similar way to Newton’s laws (the second law in particular) in classical mechanics. Bit the square of the absolute value of the wave function is nothing but the probability density. The origin of the coordinate system is fixed at the nucleus. Question 3: The square of the absolute value of a wave function gives the following quantity_.Įxplanation: The wave function is not physically significant. the sum of kinetic energy and potential energy is obtained as an eigenvalue. When it is operated on a wave function, total energy i.e. Question 2: Hamiltonian operator is a _.Įxplanation: Hamiltonian operator is an energy operator.

Question 1: In quantum mechanics, it is impossible to measure the position and momentum _.Įxplanation: According to Heisenberg’s uncertainty principle, the fundamental nature of a quantum system is that it is impossible to observe the position and momentum both accurately and simultaneously. Where E n is the energy of the nth state. Where A is the amplitude of the wave function. Hence the wave function of the particle inside the box is given as, The term kl is a multiple of π since sin ( n π ) = 0. The solution of the above equation is as follows, Which is a second-order differential equation. Let us apply the Schrödinger wave equation to the particle inside the box. Hence, the particle cannot exist outside the box. In the one-dimensional box, the electron is free which means the net potential inside the box is zero. Consider an electron of mass m in a one-dimensional box. One dimensional box is a simple system on which the Schrödinger equation can be applied to obtain the various state. The energy operator is defined as follows, The momentum operator is defined as follows, There are various quantum-mechanical operators like energy operator, position operator, and angular momentum operator, etc. The quantity p is called the eigen value of the position operator. The momentum operator can be operated on the wavefunction as follows, In Hilbert space, each state of the quantum system can be expressed using state vectors.Ĭonsider a wave function ψ ( x, t ), let p ^ be the momentum operator. The complex functions are defined in Hilbert space. Obtain the energy eigenvalues and plot the corresponding wavefunctions. The operators are defined using complex functions. Aim-Solve the s-wave Schrodinger equation for the ground state and the first excited state of the hydrogen atom: Here, m is the reduced mass of the electron. The operators are also called eigenoperators. The obtained quantity is called the eigenvalue. When a particular operator is operated with the wave function the quantity associated with the operator is obtained.
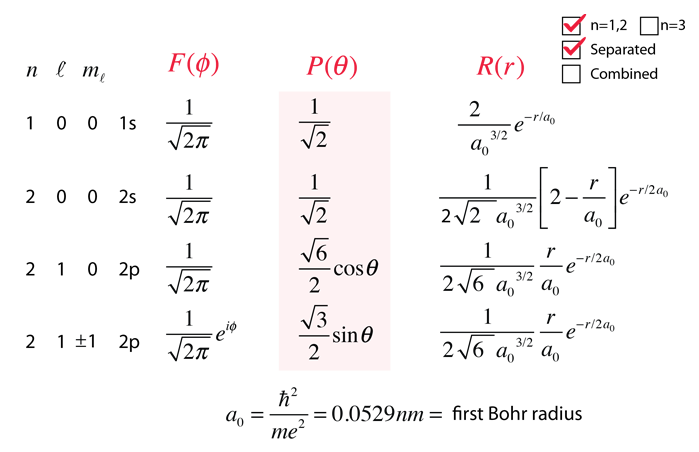
In quantum mechanics, the quantities like position, momentum, and energy can be assigned to operators. P is the probability of finding the particle in the coordinate x. The probability density P is given as follows, The wave function is usually represented using the Greek letter ψ or Ψ. The square of the absolute wave function gives the probability of finding a particle at some region of space. A wave function gives complete information about the particle. Hence particles are treated as waves this property is also called wave-particle duality. In quantum physics, it is impossible to get the exact position of any particles. The quantum particles like electrons, photons obey this uncertainty rule. This property is known as Heisenberg's uncertainty principle. In a quantum mechanical system, particles have wave-like nature.įor the particles like electrons, protons, and photons the position and momentum cannot be observed simultaneously and accurately. But it is not the case in quantum mechanics. In classical mechanics, if we know the position and momentum of the object at some point in time then we can predict the position and momentum in the future. Let us assume that an object of a certain mass is moving with a certain velocity.


 0 kommentar(er)
0 kommentar(er)
